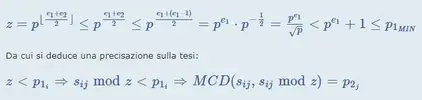@BAT vedo che non demordi (https://www.youtube-nocookie.com/embed/ocwSX3lTjpI?start=64&end=71)!

Non voglio offendere nessuno, ma hai dato l'ennesima riprova che non comprendi i contorni del problema e non capisci quello che scrivo... e te lo dimostro!
Come già detto,
la "chiave" di cui parlo nella mia dimostrazione è legata agli intervalli (nel senso che fattorizza
qualsiasi semiprimo costituito dal prodotto di una generica coppia di primi prelevati dai due intervalli) e non al singolo semiprimo
S=A*B .
Fatta questa dovuta premessa, c'è da dire che nel
tuo inutilmente lungo post, sì che hai scoperto l'acqua calda... relativamente al singolo semiprimo infatti vale quanto già avevo detto in modo più conciso
in un mio precedente post:
- le chiavi
c per cui
MCD(A*B , A*B mod c) = B saranno i valori nella forma
B(A-k) (e tutti i relativi divisori maggiori di
kB ) con
0<k<A/2 , essendo
A*B mod c = kB per tutte le chiavi associate ad un certo
k ;
- le chiavi
c per cui
MCD(A*B , A*B mod c) = A saranno i valori nella forma
A(B-k) (e tutti i relativi divisori maggiori di
kA ) con
0<k<B/2 , essendo
A*B mod c = kA per tutte le chiavi associate ad un certo
k .
Se invece siamo interessati alla chiave che ci consente di fattorizzare qualsiasi semiprimo costituito dal prodotto di una generica coppia di primi prelevata da due determinati intervalli, allora ovviamente il discorso cambia ed ecco spiegata la condizione
a mod c = 1 e il resto della
mia dimostrazione.
Quanto appena detto già sarebbe sufficiente per replicare al tuo sopracitato post, ma se vuoi posso anche commentare nello specifico alcune cose che hai scritto...
Tutto molto semplice, ovvio e soprattutto generale, infatti su s, p, q non è stata fatta nessuna ipotesi né posto alcun vincolo, trovi la fattorizzazione per qualunque coppia di numeri (entrambi primi, entrambi composti, un primo e un composto, possono anche essere uguali).
FALSO, usando la tua notazione, se
p=2 sarà
MCD(s , s mod (s-q)) = s . Per esempio per
s=2*2 sarà
MCD(4 , 4 mod 2) = 4 .
Ci sono infinite chiavi, ecco perché alla fine ci sbatte contro
FALSO, tralasciando il contesto in cui l'hai detto, affinché
s mod c ritorni un numero minore di
s , deve essere
c<=s , quindi le chiavi
c non possono mai essere infinite...
Penso che su
matematicamente non ti hanno risposto perché hai presentato male la questione, le premesse iniziali
sembrano scollegate dalle 2 dimostrazioni che esponi, non si capisce dove vuoi andare a parare. Invece a me quelle premesse piacevano perché dal poco che si capisce di quello che fa @piergiac-1 le elevazioni a potenza di numeri primi sono pane quotidiano.
Lo screenshot che hai postato mostra la formalizzazione da me fatta del metodo utilizzato in principio dall'autore.
Inoltre c'è da dire che tale formalizzazione è antecedente alla mia dimostrazione, infatti dalla dimostrazione si evince che quella riscontrata sperimentalmente dall'autore è solo un caso particolare rispetto alla proprietà matematica generale da me dimostrata.
Alla base del tuo ragionamento iniziale c'era un'affermazione palesemente falsa...
[...]
bastavano carta, penna e 3 secondi per verificare che se hai 15=3*5=5*3 li fattorizzi con MCD(15, 15 mod c) in almeno 2 modi:
15 mod 10 = 5 -> MCD(15,5) = 5 -> 15 = 5 * 3
15 mod 4 = 3 -> MCD(15,3) = 3 -> 15 = 3 * 5
oltre a c=10 e 4 si fattorizza anche con c=12, 6, 9,;
ovvio che ti ho bollato come sbagliata la dimostrazione, con una simile premessa mi sembrava una perdita di tempo inutile controllare il resto.
L'errore ti ha fatto ragionare su mezza verità, un mesetto buono per arrivare alla conclusione che la fattorizzazione esiste, facendo 15 passaggi di calcoli laboriosi nella prima versione e 10 nella seconda. Ti ha infatti obbligato ad imporre la condizione a mod c = 1, l'unico modo per arrivare ad ottenere il numero primo più piccolo, e da lì tutti i calcoli.
Non so perché sei andato a ripescare quest'affermazione
Il primo passo è stato quello di inquadrare meglio e formalizzare il metodo proposto dall'autore, che più o meno dovrebbe essere il seguente.
Sia p un numero primo e siano e1 > e2 e b degli interi positivi. Sia poi z = p^[(e1+e2)/2] (dove le parentesi quadre indicano in questo caso la divisione intera), mentre p1 e p2 sono due generici numeri primi appartenenti rispettivamente agli intervalli [p^e1 + 1 ; p^e1 + 2^b] e [p^e2 + 1 ; p^e2 + 2^b] . Si afferma che determinati valori di p, e1, e2 e b individuano una famiglia di semiprimi s = p1*p2 (costituiti cioè dal prodotto di due primi prelevati da ciascuno dei suddetti due intervalli) per cui la formula MCD(s , s mod z) fornisce la fattorizzazione del semiprimo (restituendo il MCD o p1 o p2 ). Fine.
Non starò qui a tediarvi con tutti i passaggi, mi limito quindi a dire che, ragionando matematicamente su quanto appena scritto, ho dedotto che il suddetto MCD non può restituire il maggiore dei due numeri primi (ossia p1), quindi qualora il metodo fosse corretto dovrà per forza essere
a) MCD(s , s mod z) = MCD(p1*p2 , p1*p2 mod z) = p2
che rappresenta un passaggio intermedio ormai superfluo che mi ha aiutato a passare dall'enigmatico metodo dell'autore alla mia dimostrazione, ma ti devo contraddire sul fatto che sia "palesemente falsa", sull'altro sito infatti l'ho anche dimostrata:
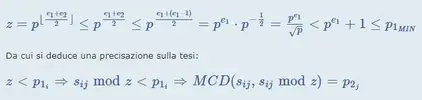
Infine dovresti ancora chiarire i seguenti due punti:
1)
invece la "dimostrazione" di @M1n021 non porta a nulla
L'hai capito che una cosa è trovare una chiave per fattorizzare un singolo semiprimo, un'altra è trovare una chiave che funzioni per più semiprimi contemporaneamente?
La mia dimostrazione fa la seconda cosa, definendo chiave e intervalli in cui funziona... a tal proposito ricordo ancora un tuo vecchio post:
Ci saranno altri numeri primi che una struttura non ce l'hanno (oppure ce l'hanno ma è diversa da quella con cui sono generati p e q); come diavolo puoi credere/pretendere che la chiave z nel modulo fattorizzi pure semiprimi generati con quelli? deve essere veramente magica se ne basta una, sempre quella, sempre la stessa, per domarli tutti, manco fosse il Signore degli Anelli.
Assurdo no? Questa non è matematica, è fantascienza.
2)
conclusione: del tuo arzigogolato meccanismo non funziona una mazza, a partire dalla "formula" per determinare gli insiemi alle "chiavi" -> la dimostrazione è sbagliata
Ne sei ancora convinto dopo che
qui ho smontato le tue obiezioni e
qui ti ho fornito tutti gli esempi che vuoi?