troverete tutte le informazioni sul sito
www.gc57crypto.net
L'ho riletto in modo più approfondito e ci ho ragionato un po' al fine di individuare una spiegazione più matematica al procedimento descritto. Premetto però che molti punti mi sono ancora oscuri (non so se per carenze mie nel comprendere o per carenze tue nell'esprimerti).
Da quello che ho capito, l'idea di fondo è quella di eseguire il processo di fattorizzazione del semiprimo
s=p*q ricercando un multiplo
m di
p o
q attraverso il calcolo di
MCD(s,m) per diversi valori di
m (in realtà tu calcoli
MCD(s-m,m), ma, essendo
(s-m)+m=s ed essendo in generale
MCD(a,b)=MCD(a+b,b), non cambia niente). Tale ricerca si fermerà al valore
m' di
m tale che
1<MCD(s,m')<s, infatti, avendo
s solo due divisori propri, sarà evidentemente
MCD(s,m') uguale a
p o
q.
Tutto si riduce quindi alla successione di valori
m da testare. Banalmente potrei partire da
m=2 e incrementare di un'unità ogni volta, fino ad arrivare ad
m'=MIN(p,q), ma evidentemente non sarebbe molto performante. Nel tuo caso gli
m da testare sono dati dalla seguente successione:
m(k) = s % |sqrt(s)| + k * |sqrt(s)| con
k=0,1,2,...
In pratica si parte da
s % |sqrt(s)| e si avanza con passo
|sqrt(s)|. Il perché di questa formulazione non mi è chiara (magari riprenderemo il discorso in seguito), ma in ogni caso, tralasciando l'efficienza, l'algoritmo funziona, in quanto esisterà sicuramente un
k'< MIN(p,q) per cui sarà
m(k')=m'.
Al fine di completare la dimostrazione matematica (non so quanto rigorosa

) dell'algoritmo, bisogna tenere conto del caso in cui
|sqrt(s)| è un multiplo di
s (vedi per esempio
s=4 e
s=143).
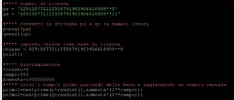
Di seguito un codice in C che tiene conto di quanto appena detto:
C:
#include <stdio.h>
#include <math.h>
unsigned int mcd_euclide(unsigned int a, unsigned int b)
{
if(a && b)
{
unsigned int r;
while(r = a % b)
{
a = b;
b = r;
}
return b;
}
return a + b;
}
unsigned int fattorizza_semiprimo(unsigned int s)
{
unsigned int y = (unsigned)sqrt(s);
unsigned int m = s % y;
unsigned int p;
if(!m)
{
return y;
}
for(;(p = mcd_euclide(s, m)) == 1; m += y);
printf("VALORE INIZIALE -> %u\n", s % y);
printf("PASSO -> %u\n", y);
printf("NUMERO ITERAZIONI -> %u\n", (m - s % y) / y + 1);
return p;
}
int main()
{
unsigned int s = 779;
unsigned int p_1 = fattorizza_semiprimo(s);
printf("\n%u=%u*%u\n", s, p_1, s / p_1);
}
Correttezza e
completezza sembrano rispettate, sull'efficienza ho molti dubbi se si escludono casi appositamente creati!

Ditemi se siete d'accordo su quanto scritto, poi magari passiamo al resto.