da cui si deduce che non è proprio una formula da media ma da superiori.... e il tasso è?
Confermando sostanzialmente l'analisi di
@Andretti60 e poste le necessarie ipotesi aggiuntive, supponiamo che il giorno 01/01/2016 "impieghi" il capitale iniziale Ci=2000€ ad un tasso periodale (il periodo d'impiego è di 1 anno e il tasso percentuale è annuale, in modo da rendere omogenee le unità di misura) i, dopo 2 anni (quindi al 31/12/2017) avrai un "montante" M=2000*(1+i)^2 (siamo in regime di interesse composto, per cui gli interessi vengono capitalizzati alla fine di ciascun periodo e contribuiscono alla valutazione degli interessi nei periodi successivi) :asd:
Ora, il giorno 01/01/2018 versi ulteriori 1000€ che vanno ad aggiungersi al montante precedente, già maturato, formando un nuovo capitale iniziale :sisi:
Nell'ipotesi che il tasso d'interesse sia lo stesso dell'operazione precedente, dopo 1 anno (al 31/12/2018) avremo: (2000*(1+i)^2 + 1000)*(1+i) = 3100 :sisi:
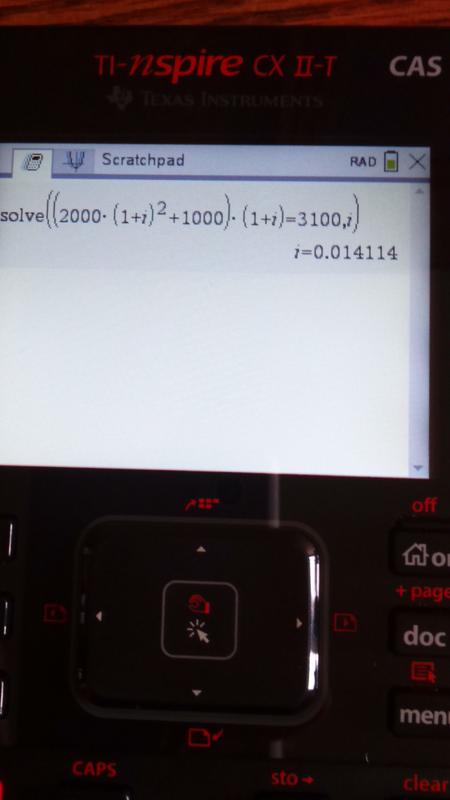
Il tasso d'interesse è i=0.014, ossia l'1.4% (annuale), con le ipotesi considerate.
Voglio fare presente che non necessariamente i tassi d'interesse sono gli stessi in tutte le operazioni di impiego di capitali e che non necessariamente la capitalizzazione degli interessi avviene negli stessi periodi di quelli a cui si riferisce il tasso; per fare un esempio, una banca può eseguire, come spesso accade nella gestione dei conti correnti, una capitalizzazione trimestrale ad un tasso d'interesse annuale, vale a dire che il periodo di capitalizzazione non coincide con quello di riferimento del tasso d'interesse.
Ciao, a presto :sisi:

