- 3,567
- 629
- CPU
- Intel i5 12600K stock
- Dissipatore
- Noctua NH-U12S
- Scheda Madre
- Gigabyte Z690 UD
- HDD
- SK hynix Platinum P41 2TB + Crucial MX300 525GB+ Samsung Evo850 250GB + WD Green 3TB
- RAM
- Corsair Vengeance DDR5 32GB @ 5800Mhz
- GPU
- Nvidia 4070 Pny
- Monitor
- AOC Q27G2U WQHD 2560 x 1440 @ 144 Hz
- PSU
- Enermax REvolution D.F. 850W
- Case
- Thermaltake Chaser MKI
- Periferiche
- Nas DS918+
- Net
- Wifi4all Hyperlan 50/5 FTTW
- OS
- Win11
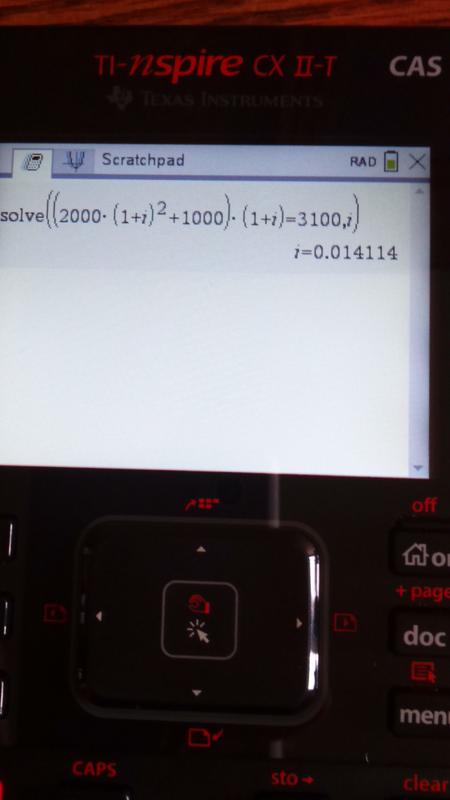
Potrà sembrare facile per alcuni... per me no :) Sembra un compito di matematica delle medie ma non riesco a venirne fuori.
Nel 2016 ho investito 2.000 (cifra ipotetica) e nel 2018 ho aggiunto 1.000
Se adesso in totale mi ritrovo 3.100 che interesse % ho avuto?
Nel 2016 ho investito 2.000 (cifra ipotetica) e nel 2018 ho aggiunto 1.000
Se adesso in totale mi ritrovo 3.100 che interesse % ho avuto?