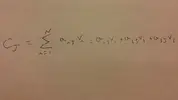RISOLTO Vector - Matrix multiplication

[Marcus Aseth]

Mi scuso se anche questa domanda ha più a che fare con matematica che programmazione, ma è l'esempio riportato sul libro "3d game programming with directx 11" quindi in un certo senso è legato alla computer grafica e quindi spero di non essere troppo off topic.

Adesso alla mia domanda, dato un vettore 3D "u = {x,y,z}" ed una matrice 3x3 chiamata "A" , la moltiplicazione del vettore "u" per la matrice "A" equivale alla formula riportata nell'immagine sotto:

ed il libro da anche la formula finale

uA = xA1, * + yA2, * + zA3, *

(stessa cosa dell'ultima riga nell'immagine precedente).

Adesso, capisco il significato delle prime 2 righe dell'imagine, ovvero il risultato dell'operazione "uA" è un nuovo vettore con elementi x,y,z uguali al dot product tra il vettore "u" ed il "column vector"(della matrice) 1,2,3 rispettivamente.

Quindi il vettore risultante (chiamiamolo "v") sarebbe "uA = v = { x = u・(A*,1), y = u・(A*,2), z = u・(A*,3) }"

Fin qui tutto chiaro, ma se poi andiamo a vedere la terza, quarta e quinta riga dell'immagine, ragruppa le x,y,z e somma tutto assieme con quella formula
"uA = xA1, * + yA2, * + zA3, *"
Non riesco a ricollegare queste 2 cose, perchè nelle prime 2 righe otteniamo un vettore3D, sommando tutto otteniamo un singolo numero che ho controllato e non corrisponde neppure alla lunghezza del vettore "v".

Quindi potreste spiegarmi il senso della terza fino alla quinta riga? Qual'è il senso di "uA = xA1, * + yA2, * + zA3, *" ed a cosa serve il singolo numero ritornato, ed ancora, perchè uA è uguale ad esso se uA è un vettore 3D?

 

[BAT]

Hai un grosso problema:
invece di studiare l'algebra delle matrici su un libro di (guarda un po'!) algebra, ti stai affidando ad un libro di programmazione che evidentemente dà per scontato che tu ne sappia già qualcosa di calcolo matriciale.
Il prodotto fra matrici è definito come "righe per colonne" e non c'è bisogno di imparare nessuna formula per eseguirlo, ma solo capire come si fa.
Innanzitutto la prima cosa da capire è QUANDO è possibile farlo:
date 2 matrici
A(m,n) = matrice con m righe ed n colonne
B(p,q) = mat. con p righe e q colonne
- la moltiplicazione è possibile se solo se n=p cioè quando il numero di colonne di A è uguale al numero di righe di B
- il risultato è una matrice C(m,q) cioè ha lo stesso numero di righe di A e lo stesso numero di colonne di B
Questo implica anche che la proprietà commutativa per le matrici non vale, in particolare
- innanzitutto se è possibile fare AxB non è detto che sia possibile fare BxA
- se sono possibili sia AxB che BxA il risultato del prodotto dà generalmente matrici diverse
Altra cosa da sapere è COME si fa il prodotto: se C è la matrice risultante, il suo elemento generico c[i,j] (riga i e colonna j) è definito dalla somma dei prodotti della i-esima riga di A per la j-esima colonna di B (se preferisci è il prodotto scalare della riga A(i) per la colonna B(j) )
Nella figura che hai postato A1, A2, A3 sono le colonne della matrice A sebbene come notazione sia balorda
nel tuo caso facciamo che
u=(1,2,3)
A= te la scrivo incolonnata e metto in colori diverse le colonne
1 2 3
4 5 6
7 8 9
allora le dimensioni sono u(1,3), A(3,3) quindi il risultato del prodotto è una matrice C(1,3) cioè con 1 riga e 3 colonne
il prodotto uA si fa righe di A per colonne di B
uA= ( (1,2,3)*(1,4,7) , (1,2,3)*(2,5,8) , (1,2,3)*(3,6,9) ) =
= ( 1*1+2*4+3*7 , 1*2+2*5+3*8, 1*3+2*6+3*9 ) =
= (30, 36, 42)

P.S
nota che NON si può moltiplicare B(3,3) per u(1,3)
per farlo u dovrebbe essere un vettore colonna (3,1)=3 righe e 1 colonna

 

[Marcus Aseth]

Bat00cent ti ringrazio per aver preso il tempo per scrivere ciò, però tutto quello che hai scritto mi è gia chiaro (tutto spiegato nel libro 3d game programming using directx 11, non introduce DX11 primo di pagina 150 mi pare, tutto spiegazione di vettori e matrici quindi prima di DX11), infatti sotto puoi vedere che avevo gia scritto tutto il codice necessario (seppur non ottimale, fatto solo per vedere i risultati) ed inserendo i tuoi numeri, ottengo lo stesso risultato(codice con output sotto).

E volendo posso farlo anche a mano senza problemi perchè a punto ho capito il procedimento.
Tutto ciò non spiega la riga 3,4,5 nell'immagine del primo reply, pecui chiunque voglia spiegare quelle e rispondere alla mia domanda, rimando al primo messaggio in alto alla pagina :)

#include <iostream>
#include <initializer_list>
#include <iterator>
using namespace std;

#define PI 3.14159265358979
constexpr double toDeg(const double rad) { return rad * (180 / PI); }
constexpr double toRad(const double deg) { return deg * (PI / 180); }

class Vector {
public:
    //constructors
    Vector(double _x, double _y, double _z) : x{ _x }, y{ _y }, z{ _z } { magnitude = computeMagnitude(); }
    Vector(double deg, double _magnitude = 1) : z{ 0 } {
        x = _magnitude * cos(toRad(deg));
        y = _magnitude * sin(toRad(deg));
        magnitude = _magnitude;
    }

    //Methods
    inline double computeMagnitude() {
        magnitude = sqrt(x*x + y*y + z*z); return magnitude;
    }

    inline void normalize() {
        computeMagnitude();
        x = x / magnitude; y = y / magnitude; z = z / magnitude;
    }

    inline double angleBetween(Vector& v1, Vector& v2) {
        return acos(Vector::dotProduct(v1, v2) / (v1.computeMagnitude() * v2.computeMagnitude()));
    }

    inline void orthogonalization(Vector v2) {
        this->x = x - (this->magnitude * cos(angleBetween(*this, v2)));
    }

    //Static Method
    static inline double dotProduct(const Vector& v1, const Vector& v2) {
        return v1.x*v2.x + v1.y*v2.y + v1.z*v2.z;
    }

    static inline Vector crossProduct(const Vector& v1, const Vector& v2) {
        return Vector(
            v1.y*v2.z - v1.z*v2.y, //X
            v1.z*v2.x - v1.x*v2.z, //Y
            v1.x*v2.y - v1.y*v2.x  //Z
        );
    }

    //Variables
    double x;
    double y;
    double z;
    double magnitude;

    //Overloaded Operators
    friend ostream& operator<<(ostream&, const Vector&);
    friend Vector operator+(const Vector&, const Vector&);
    friend Vector operator-(const Vector&, const Vector&);
};

class Matrix3x3 {
public:
    Matrix3x3() {}
    Matrix3x3(initializer_list<double> val) {
        if (val.size() == 9)
        {
            initializer_list<double>::iterator it = val.begin();
            for (size_t i = 0; i < 3; i++)
            {
                for (size_t j = 0; j < 3; j++)
                {
                    matrix[i][j] = *it++;
                }
            }
        }
    }
    inline double getVal(unsigned i, unsigned j) const { return matrix[i][j]; }
    inline void setVal(unsigned i, unsigned j, double val) { matrix[i][j] = val; }
private:
    double matrix[3][3];
};

ostream& operator<<(ostream& stream, const Vector& v)
{
    return stream << "x,y,z{" << v.x << "," << v.y << "," << v.z << "} |magnitude| = " << v.magnitude;
}
Vector operator+(const Vector& lhs, const Vector& rhs)
{
    return Vector(lhs.x + rhs.x, lhs.y + rhs.y, lhs.z + rhs.z);
}
Vector operator-(const Vector& lhs, const Vector& rhs)
{
    return Vector(lhs.x + (-rhs.x), lhs.y + (-rhs.y), lhs.z + (-rhs.z));
}
ostream& operator<<(ostream& stream, const Matrix3x3& m)
{
    for (size_t i = 0; i < 3; i++)
    {
        stream << "| ";
        for (size_t j = 0; j < 3; j++)
        {
            stream << m.getVal(i, j) << " , ";
            if (j == 2) { stream << "|" << endl; }
        }
    }
    return stream;
}
Matrix3x3 operator*(const Matrix3x3& M1, const Matrix3x3& M2)
{
    Matrix3x3 result;
    for (size_t i = 0; i < 3; i++)
    {
        for (size_t j = 0; j < 3; j++)
        {
            Vector v1(M1.getVal(i, 0), M1.getVal(i, 1), M1.getVal(i, 2));
            Vector v2(M2.getVal(0, j), M2.getVal(1, j), M2.getVal(2, j));
            result.setVal(i, j, Vector::dotProduct(v1, v2));
        }
    }
    return result;
}
Vector operator*(const Vector& v, const Matrix3x3& M)
{
    Vector result(0, 0, 0);
    result.x = Vector::dotProduct(v, Vector(M.getVal(0, 0), M.getVal(1, 0), M.getVal(2, 0)));
    result.y = Vector::dotProduct(v, Vector(M.getVal(0, 1), M.getVal(1, 1), M.getVal(2, 1)));
    result.z = Vector::dotProduct(v, Vector(M.getVal(0, 2), M.getVal(1, 2), M.getVal(2, 2)));
    return result;
}

int main()
{
    Vector u = { 1, 2, 3 };    Matrix3x3 A={
                                          1 , 2 , 3 ,
                                          4 , 5 , 6 ,
                                          7 , 8 , 9
                                        };

    Vector v = u*A;


    cout << v << endl;
 
    return 0;
}

output:

x,y,z{30,36,42}

 

[BAT]

quelle sono solo notaziani e svolgimento dei calcoli: u è scomposto in u=(x,y,z)
la riga 3 ha semplicemente diviso in 3 vettori le somme esplicite della riga 2, in modo da mettere x in un vettore, y in un altro e z nell'ultimo
la riga 4 raccoglie a fattor comune quanto fatto in riga 3 perchè, per es, (xA[1,1], xA[1,2], xA[1,3] = x ( A[1,1], A[1,2], A[1,3] ) e così per gli altri 2
la riga 5 è una notazione (un po' balorda secondo me) per dire che il risultato è un vettore a 3 componenti dove
la prima componente è data da x moltiplicata per la prima riga di A indicata con A[1,*] che è una riga non un singolo numero, così per le altre 2 componenti.
In pratica ha fatto il calcolo con
1(1,2,3)+2(4,5,6)+3(7,8,9)=(1,2,3)+(8,10,12)+(21,24,27)=(30,36,42)
suppongo che questo modo di fare i calcoli sia ristretto al particolare caso della grafica 3D

 

[rodhellas]

Hai una matrice ixj e un vettore riga, il prodotto di uA sarà C dove: . Guarda le regole del prodotto tra matrici e vettori

 

[Marcus Aseth]

quelle sono solo notaziani e svolgimento dei calcoli: u è scomposto in u=(x,y,z)
la riga 3 ha semplicemente diviso in 3 vettori le somme esplicite della riga 2, in modo da mettere x in un vettore, y in un altro e z nell'utlimo
la riga 4 raccoglie a fattor comune quanto fatto in riga 3 perchè, per es, (xA[1,1], xA[1,2], xA[1,3] = x ( A[1,1], A[1,2], A[1,3] ) e così per gli altri 2
la riga 5 è una notazione (un po' balorda secondo me) per dire che il risultato è un vettore a 3 componenti dove
la prima componente è data da x moltiplicata per la prima colonna di A indicata con A[1,*] che è una colonna non un singolo numero, così per le altre 2 componenti.
Con l'esempio che ho fatto ti sta dicendo che il risultato è
1(1,2,3) + 2(4,5,6) + 3(7,8,9) =
= (1,2,3)+(8,10,12)+(21,24,27)= guarda caso (30, 36, 42)

Bingo! :D
Questo era il tassello mancante e la cosa alla quale cercavo risposta, infatti per metterlo in termini un pò piu grafici, i componenti del vettore entrano da sinistra e le somme escono da sotto, allora:

-vettore-x | x + x + x |
-vettore-y | y + y + y |
-vettore-z | z + z + z |
risultato: { x , y , z }

quindi con i numeri nel tuo esempio:
-----------1 | 1 + 2 + 3 |
-----------2 | 4 + 5 + 6 |
-----------3 | 7 + 8 + 9 |
risultato: { -- , -- , -- }

diventa:
----------------| 1 + 2 + 3 |
----------------| 8 +10 +12 |
----------------|21+24 +27 |
risultato: { 30, 36 , 42 }

ti correggo soltanto dove dici

la prima colonna di A indicata con A[1,*]

visto che A1,* indica un row vector :D

Cmq davvero grazie mille, non avanzo mai nei libri fino a che non sono sicuro di aver capito, percui adesso posso continuare ;) (e concordo, la riga 5 ha una notazione balorda :\)

 

[BAT]

Solo per precisare: avevo corretto il mio post: A[1,*] è una RIGA (non una colonna come avevo scritto inizialmente - e solo poi corretto) e così le altre due, quello che tu chiami "row vector" (immagino che ti stai uniformando linguisticamente al libro che leggi, ma sarebbe importante anche sapere la giusta denominazione in Italiano... :))

 

[Blume.]

Vi invidio....

 

[Marcus Aseth]

Vi invidio....

Lol. Tieni presente che non sapevo nulla di quello scritto in questo topic una settimana fà, ancora meno 1 mese fà o 2... il primo passo (ed anche il piu difficile) è decidere di imparare una cosa nuova, il resto è in discesa e sopratutto ne vale la pena se poi a qualche mese da ora guardi indietro a quando non capivi una cosa che adesso ti sembra ovvia.
Io mi metto a ridere se ora vado a rileggere cosa scrivevo un'anno fà quando ero confuso da dei video di programmazione perchè usavano "variabili" xD

 

[DispatchCode]

Il prossimo passo potrebbe essere, anche solo per fini di studio, modificare il codice utilizzando le intrinsics - o asm inline - per sfruttare il calcolo in parallelo con i registri XMM; in alternativa potresti anche compilare con -sse4.2, e verificare se vengono già utilizzate.
Su matrici molto piccole e calcoli non ripetuti le differenze potrebbero anche non notarsi; ma su matrici più importanti farebbero la differenza.

 

[Marcus Aseth]

Il prossimo passo potrebbe essere, anche solo per fini di studio, modificare il codice utilizzando le intrinsics - o asm inline - per sfruttare il calcolo in parallelo con i registri XMM; in alternativa potresti anche compilare con -sse4.2, e verificare se vengono già utilizzate.
Su matrici molto piccole e calcoli non ripetuti le differenze potrebbero anche non notarsi; ma su matrici più importanti farebbero la differenza.

Il libro che sto leggendo si appoggia su DirectXMath quindi ora uso un pò quella per farmi un'idea generale di com'è una classe Matrix seria, ma in futuro probabilmente tornerò sulla mia come esercizio e proverò a mettere in pratica, grazie del suggerimento :)

Tra l'altro, parentesi a parte, ho portato un pò avanti la mia classe per permettere la creazione di matrici di dimensioni arbitrarie e aggiunto una funzione "double Matrix::_determinant(Matrix & M)" recursiva per trovare la determinante di matrici di qualsiasi dimensione xD Codice sotto per i curiosi :)

#include "Matrix.h"
#include <iostream>

Matrix minorMatrix(Matrix& M, unsigned _i, unsigned _j)
{
    //Check if _i and _j are valid numbers
    _i = _i < M.rows() ? _i : 0;
    _j = _j < M.columns() ? _j : 0;

    //Create matrix (n-1 * n-1)
    Matrix mM(M.rows() - 1, M.columns() - 1, {});

    if (M.rows() == 1 && M.columns() == 1)
    {
        return M; //if 1x1 matrix, return it
    }
    else
    {
        unsigned I = 0, J = 0;
        for (size_t i = 0; i < M.rows(); i++)
        {
            for (size_t j = 0; j < M.columns(); j++)
            {
                if (i != _i && j != _j) //skip row _i elements, column _j elements
                {
                    mM.matrix()[I][J++] = M.matrix()[i][j]; //add valid elements and increase J
                    if (J == mM.columns()) { I++; J = 0; } // if J is 1 past the end, go next row
                }
            }
        }
    }
    return mM;
}

Matrix::Matrix(unsigned rows, unsigned columns, std::initializer_list<double> elements)
{
    //smallest matrix possible must be 1x1
    _rows = rows <= 0 ? 1 : rows;
    _columns = columns <= 0 ? 1 : columns;
    _matrix = std::make_shared<Array2D>();
    //set matrix size
    _matrix->resize(_rows);
    for (auto& row : *_matrix)
    {
        row.resize(_columns);
    }
    //fill matrix
    auto iterator = elements.begin();
    for (size_t i = 0; i < _rows; i++)
    {
        for (size_t j = 0; j < _columns; j++)
        {
            double currentVal = iterator != elements.end() ? *iterator++ : 0;
            (*_matrix)[i][j] = currentVal;
        }
    }
}

double Matrix::determinant()
{
    return _determinant(*this);
}


double Matrix::_determinant(Matrix & M)
{
    // if matrix not square, return 0
    if (_rows != _columns) { return 0; }
 
    //solve for 2x2 Matrix
    if (M.rows() == 2) { return M.valueFromMinorMatrix(); }

    //recursively find determinant
    double determinant{};
    unsigned n = M.rows();
    int sign = -1;
    for (size_t j = 0; j < n; j++)
    {
        sign *= -1; //invert sign every loop
        determinant += M.matrix()[0][j] * sign * _determinant(minorMatrix(M, 0, j));
    }
    return determinant;
}

double Matrix::valueFromMinorMatrix()
{
    //make sure matrix is 2x2
    if (_rows != _columns && _columns != 2) { return 0; }
    return (((*_matrix)[0][0] * (*_matrix)[1][1]) - ((*_matrix)[0][1] * (*_matrix)[1][0]));
}

Matrix::~Matrix()
{
}

input 4x4

Matrix M(4, 4,
{ 2,-2, 3, 6,
1, 1, 1, 7,
4,12, 4, 1,
0, 2, 2, 2});

output:

determinant: 414