[C] Generare un turno di partite

Pubblicità
A

alessandro_2001

Nuovo Utente
Messaggi
3
Reazioni
0
Punteggio
19
ciao a tutti ho un problema a risolvere questo programma in c datomi dal prof di informatica:
Traccia:
Dato un vettore chiamato Squadre con n elementi (max 10 - caricati dall’utente) contenenti i nomi delle squadre che partecipano ad un torneo calcistico, generare un turno di partite accoppiando casualmente le squadre e associando risultati casuali alle partite.
I risultati casuali vanno espressi in termini di schedina ovvero 1, X o 2.
Stampare l’elenco delle partite con relativo risultato (stampare la partita sulla stessa riga del risultato tipo colonna del totocalcio).

Se sapete darmi una soluzione
Grazie in anticipo
1586263531053.png

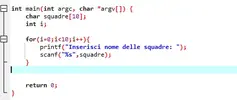
questo è dove sono arrivato se qualcuno riesce a dirmi come faccio a generare gli accoppiamenti delle squadre.
grazie
 
Ultima modifica da un moderatore:
Prime 3 righe del regolamento della sezione Programmazione:

Soluzione dei problemi
La sezione Programmazione e le sue sottosezioni non offrono un servizio di risoluzione compiti scolastici.
E' possibile chiedere aiuto ma allegando il codice scritto o le prove fatte.

Ritenta e sarai più fortunato.
 
rodhellas ha detto:
Prime 3 righe del regolamento della sezione Programmazione:

Soluzione dei problemi
La sezione Programmazione e le sue sottosezioni non offrono un servizio di risoluzione compiti scolastici.
E' possibile chiedere aiuto ma allegando il codice scritto o le prove fatte.

Ritenta e sarai più fortunato.
Clicca per espandere...
grazie
 
Ciao, ma devi generare una singola giornata o ti servono gli abbinamenti dell'intero "campionato"?
 
Posso provarti ad indurre nel ragionamento:
- Ti serve un ciclo per fare le accoppiate, ad esempio puoi provare a sfruttare l'algoritmo della ricerca binaria per fare le combinazioni, ed eventualmente stampare una casella di un altro vettore contenente i possibili risultati 1 - X - 2
- Ogni accoppiata toglie due elementi nella "lista" delle squadre
- L'accoppiata non può verificarsi se l'id squadra è lo stesso.
- Una variabile casuale, che si aggiorni ad ogni ciclo per far uscire un numero compreso tra 0 - 1 - 2 che lo userai come indice per un probabile secondo vettore per far uscire un possibile esito della giocata
 
ragionamento illogico: fare una ricerca (binaria? e chi ti dice che il vettore è ordinato) per accoppiare le squadre,...
scusa ma che ricerca vorresti fare?
il modo più semplice in assoluto è considerare il vettore come se fosse una mazzo di carte:
- generi 2 numeri interi a caso compresi tra 0 e l'ultimo indice buono del vettore (per es. per un vettore da 20 posizioni generi 2 numeri interi compresi tra 0 e 19)
- scambi la posizione delle squadre in base agli indici (in pratica: se genere 3 e 12, scambi di posto le squadre di indice 3 e 12);
- fai un numero ragionevole di questi scambi, per esempio 50 o 100
alla fine degli scambi hai "mischiato" le squadre in modo (pseudo)casuale;
alla fine l'accoppiamento è semplicemente, "le prime 2", "le seconde 2", la terza coppia" (ovvero il turno è squadra[0] contro squadra[1], squadra[2] contro squadra[3]..., squadre[18] contro squadra[19]);
avendo mischiato per bene le squadre all'inizio il turno è completamente casuale e funziona anche se lo stesso numero pseudocasuale è generato molte volte.
Alternativa:
generi 2 numeri pseudocasuali (indici), sposti le squadre generate a fine vettore e le accoppi;
ripeti il procedimento escludendo però dalla generazione casuale i 2 ultimi indici, e così via per tutti gli altri.

Per il risultato invece è più semplice, visto che il renge è limitato a 3 valori e comunque ciascun risultato è indipendente dal precedente
 
Quello di mischiare l'array e considerare le coppie successive risultanti credo sia la strada migliore.
Per quanto riguarda invece il mescolamento utilizzerei un approccio più semplice e allo stesso tempo caratterizzato da una distribuzione delle probabilità uniforme. Ossia andremo a scambiare, partendo dalla fine e avanzando verso sinistra, l'elemento corrente con un elemento preso a caso da un gruppo contenente gli elementi precedenti e l'elemento corrente.
 
BAT00cent ha detto:
ragionamento illogico: fare una ricerca (binaria? e chi ti dice che il vettore è ordinato) per accoppiare le squadre,...
scusa ma che ricerca vorresti fare?
il modo più semplice in assoluto è considerare il vettore come se fosse una mazzo di carte:
- generi 2 numeri interi a caso compresi tra 0 e l'ultimo indice buono del vettore (per es. per un vettore da 20 posizioni generi 2 numeri interi compresi tra 0 e 19)
- scambi la posizione delle squadre in base agli indici (in pratica: se genere 3 e 12, scambi di posto le squadre di indice 3 e 12);
- fai un numero ragionevole di questi scambi, per esempio 50 o 100
alla fine degli scambi hai "mischiato" le squadre in modo (pseudo)casuale;
alla fine l'accoppiamento è semplicemente, "le prime 2", "le seconde 2", la terza coppia" (ovvero il turno è squadra[0] contro squadra[1], squadra[2] contro squadra[3]..., squadre[18] contro squadra[19]);
avendo mischiato per bene le squadre all'inizio il turno è completamente casuale e funziona anche se lo stesso numero pseudocasuale è generato molte volte.
Alternativa:
generi 2 numeri pseudocasuali (indici), sposti le squadre generate a fine vettore e le accoppi;
ripeti il procedimento escludendo però dalla generazione casuale i 2 ultimi indici, e così via per tutti gli altri.

Per il risultato invece è più semplice, visto che il renge è limitato a 3 valori e comunque ciascun risultato è indipendente dal precedente
Clicca per espandere...

Tutto questo per un semplice compito?

Quello che intendevo, è di applicare più o meno la base che c'è di fondo dell'algoritmo della ricerca binaria. Dimezzi la dimensione dell'array e " ti ritrovi 5 squadre da una parte e 5 dall'altra". Poi ti diverti a giocare con gli indici, magari cambiando solo quelli della seconda fascia e ti fai una combinazione pseudocasuale. Non modifichi l'array ti limiti a stampare a schermo le combinazioni con i risultati. Meno righe di codice, eludi la traccia e fai vedere a schermo il risultato che il professore ha chiesto.

Stiamo pur parlando di un turno di campionato formato da 10 squadre, non di un programma per organizzare la serie A. Il ragazzo si è fermato all'inserimento dei dati in un array dubito possa completare al meglio ciò che hai scritto. (Senza offesa).
Mi sono espresso male, bye.
 
nardoz0918 ha detto:
Meno righe di codice,
Clicca per espandere...
Non ci metti meno righe...
Per codificare l'algoritmo (per quanto semplice) di ciò che ho scritto servono 4 righe di pseudocodice, che si tradurrano in 6 riche di codice reale a causa delle 3 necessarie ad uno scambio
1. per k che va da 0 a 50 ripeti i punti 2-3-4 (ciclo FOR)
2. p1 = genera intero casuale (con funzione incorporata nel linguaggio ovviamente)
3. p2 = genera intero casuale
4. scambia squadra[p1] con squadra[p2]

procedendo come suggerisci (circa la stessa cosa di @M1n021) non si rispettano le specifiche del problema:
se hai un array da 10 elementi e lo dividi in 2 gruppi di 5 squadre, poi gli accoppiamenti, anche se casuali, li fai solo tra una squadra del primo gruppo ed una del secondo gruppo.
Il che significa che impedisci a squadre dello stesso gruppo di giocare tra di loro, quindi il turno non è affatto casuale.
Inoltre, ben che ti vada, non è neanche possibile che ci metti meno righe!
Infine, nota che la bontà di un metodo/algoritmo non si misura con chi scrive meno righe, ma con il fatto che esso sia corretto (cioò che funzioni) e completo (cioè che includa tutti i possibili casi del problema in esame).
 
Ultima modifica:
Mah... se si tratta di generare un solo turno con risultati casuali degli incontri e senza alcun tipo di vincolo, direi che il problema posto è estremamente banale, quindi non vedo motivo alcuno per complicarlo.

L'associazione può avvenire semplicemente di un elemento del vettore con il successivo percorrendolo su tutti gli indici dispari, ad ogni associazione aggiungere un valore casuale (range int 0..2) quale risultato.
Se si vuole rendere non controllabile l'associazione con l'inserimento manuale delle squadre allora serve (come dice @BAT00cent ) dare qualche mescolata al contenuto del vettore prima di fare l'associazione.

Inserire -> mescolare -> e infine, associare il tutto in un vettore che contiene le due squadre dell'incontro e il risultato della partita!

Inviato dal mio Nexus 6P utilizzando Tapatalk
 
Boh per me esercizietti stupidi richiedono un metodo risolutivo stupido. Non stiamo parlando di una lista esagerata di squadre ma di 10 squadre non ha importanza se fai una combinazione con le prime 5 e lee altre 5 casualmente. Così l'ho interpretata io la traccia.

Poi per favore non possiamo minimamente parlare della "bontà" di un algoritmo per quest'esempio.(Sono d'accordissimo con te)
 
nardoz0918 ha detto:
Boh per me esercizietti stupidi richiedono un metodo risolutivo stupido. Non stiamo parlando di una lista esagerata di squadre ma di 10 squadre non ha importanza se fai una combinazione con le prime 5 e lee altre 5 casualmente. Così l'ho interpretata io la traccia.

Poi per favore non possiamo minimamente parlare della "bontà" di un algoritmo per quest'esempio.(Sono d'accordissimo con te)
Clicca per espandere...
Non sono d'accordo. La bontà dell'algoritmo deve esserci sempre e non si tratta di un esercizio "stupido" ma bensì di un esercizio molto semplice.
Parlando di "algoritmo", il fatto che ci possa essere 1 milione di elementi nel vettore non rende l'esercizio più difficile, ma fa apprezzare proprio il fatto che un algoritmo dovrebbe essere sempre ottimizzato.

Inviato dal mio Nexus 6P utilizzando Tapatalk
 
rctimelines ha detto:
Non sono d'accordo. La bontà dell'algoritmo deve esserci sempre e non si tratta di un esercizio "stupido" ma bensì di un esercizio molto semplice.
Parlando di "algoritmo", il fatto che ci possa essere 1 milione di elementi nel vettore non rende l'esercizio più difficile, ma fa apprezzare proprio il fatto che un algoritmo dovrebbe essere sempre ottimizzato.

Inviato dal mio Nexus 6P utilizzando Tapatalk
Clicca per espandere...

Sto solamente affermando il fatto che per un vettore di 10 elementi è superfluo parlare di bontà. Poi credo siano punti di vista.
 
Non è una questione di 10, 20 o 1000 elementi. La stesura di qualsiasi algoritmo, , è che sia, per quanto possibile, corretto e completo; inoltre, dovrebbe essere efficiente.
Corretto = deve fare esattamente ciò che il problema richiede;
completo = deve essere applicabile a qualunque ISTANZA del problema (indipendente, nei limiti del possibile, alla dimensione dell'input);
efficiente = deve risolvere il problema nel minor tempo possibile.
Se non applichi questi principi ai problemi facili, diventi un cattivo programmatore, ti perdi i casi particolari, trascuri le dimensioni, trascuri l'ottimizzazione.
A maggior ragione, anche se un esercizio è banale, non bisogna risolverlo per forza in modo banale. Sforzarsi di fare meglio sugli esercizi facili ti dà la forma mentis per farlo anche su quelli complicati. E' un invito a pensare "posso fare meglio!". E se puoi farlo meglio, DEVI farlo meglio!
 
Pubblicità
Pubblicità
Indietro
Top